UNIDAD 1: Fundamentos de sistemas numéricos y codificación binaria.

 Tema 3: Sistemas numéricos digitales

En la tecnología digital se utilizan muchos sistemas numéricos. Los más comunes son los siguientes: decimal, binario, octal y hexadecimal. Evidentemente el sistema decimal es el más conocido, ya que es el que utilizamos a diario. Analicemos algunas de sus características para ayudarnos a comprender los demás sistemas numéricos.    

    Sistema Decimal

El sistema decimal está compuesto de 10 números o símbolos. Estos 10 símbolos son: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9;  al utilizar estos símbolos como dígitos de un número, podemos expresar cualquier cantidad. El sistema decimal se conoce también como sistema de base 10 ya que tiene 10 dígitos, y ha evolucionado en forma natural debido al hecho de que las personas tenemos 10 dedos. De hecho, la palabra dígito se deriva de la palabra “dedo”.

El  decimal  es  un  sistema  de  valor  posicional,  en  el  cual  el  valor  de  un  dígito depende de su posición. Por ejemplo, considere el número decimal 453. Por la posición de los dígitos sabemos que el 4 en realidad representa 4 centenas, el 5 representa 5 decenas y el 3 representa 3 unidades. En esencia, el 4 lleva el mayor peso de los tres dígitos y se le conoce como el dígito más significativo (MSD) mientras que el 3 lleva el menor peso y se le conoce como el dígito menos significativo (LSD).

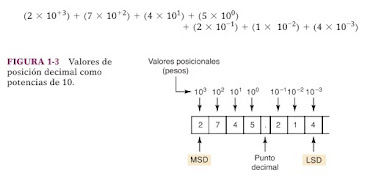
Dicho de forma más rigurosa, las diversas posiciones relativas al punto decimal llevan  pesos  que  pueden  expresarse  como  potencias  de  10.  Esto  se  ilustra  en  la figura 1-3, en donde se representa el número 2745.214. El punto decimal separa las potencias positivas de 10 de las potencias negativas. El número 2745.214 es, por lo tanto, igual a:

Subtema 1: Representación de cantidades binarias

     Sistema Binario

Desafortunadamente,  el  sistema  numérico  decimal  no  se  presta  para  una  implementación conveniente en los sistemas digitales. Por ejemplo, es muy difícil diseñar equipo electrónico de manera que pueda trabajar con 10 niveles de voltaje distintos (cada uno representando un carácter decimal, del 0 al 9). Por otro lado, es muy sencillo diseñar circuitos electrónicos simples y precisos que operen sólo con dos niveles de voltaje. Por esta razón casi cualquier sistema digital utiliza el sistema numérico binario (base 2) como el sistema numérico básico de sus operaciones. Frecuentemente  se  utilizan  otros  sistemas  numéricos  para  interpretar  o  representar cantidades  binarias,  para  ayudar  a  las  personas  que  trabajan  con  estos  sistemas digitales y los utilizan.

En el sistema binario sólo hay dos símbolos o posibles valores de dígitos: 0 y 1. Aún así, este sistema de base 2 puede usarse para representar cualquier cantidad que pueda representarse en decimal o en otros sistemas numéricos. Sin embargo, se requeriría de un mayor número de dígitos binarios para expresar una determinada cantidad.

Todas las aseveraciones mencionadas con respecto al sistema decimal pueden aplicarse de igual forma al sistema binario. Este sistema también es de valor posicional, en donde cada dígito binario tiene su propio peso expresado como potencia de 2. Esto se ilustra en la figura 1-5, donde los lugares a la izquierda del punto binario (contraparte del punto decimal) son potencias positivas de 2, y los lugares a la derecha son potencias negativas de 2. El número 1101.101 se representa en la figura. Para encontrar su equivalente en el sistema decimal, sólo tomamos la suma de los productos del valor de cada dígito (0 o 1) y su valor posicional.

        Subtema 2: Transmisión en serie y paralelo

Una de las operaciones más comunes que ocurre en cualquier sistema digital es la transmisión de información de un lugar a otro. La información puede transmitirse a través de una distancia tan pequeña como una fracción de un centímetro en la misma  tarjeta  de  circuitos,  o  a  través  de  muchos  kilómetros  cuando  el  operador de una terminal de computadora se comunica con una ubicada en otra ciudad. La información que se transmite se encuentra en formato binario y, por lo general, se representa como voltajes en las salidas de un circuito emisor, las cuales se conectan a las entradas de un circuito receptor. La figura 1-10 ilustra los dos métodos básicos para la transmisión de información digital: en paralelo y en serie.

la palabra “Hi” en la computadora. El código binario para la “H” es 01001000 y el código binario para la “i” es 01101001. Cada carácter (la “H” y la “i”) está formado de ocho bits. Mediante el uso de la transmisión en paralelo, los ocho bits se envían al mismo tiempo a través de ocho alambres. La “H” se envía primero, seguida de la “i”. La figura 1-10(b) demuestra el uso de la transmisión en serie como cuando se utiliza  un  puerto  COM  serial  en  la  computadora  para  enviar  datos  a  un  módem, o cuando se utiliza un puerto USB (Bus Serie Universal) para enviar datos a una impresora. Aunque los detalles acerca de los formatos de los datos y la velocidad de la transmisión son bastante distintos entre un puerto COM y un puerto USB, los datos en sí se envían de la misma forma: un bit a la vez, a través de un solo alambre. Los bits se muestran en el diagrama como si en realidad se desplazaran sobre el alambre en el orden mostrado. El bit menos significativo de la “H” se envía primero y el bit más significativo de la “i” se envía al último. Desde luego que en la realidad sólo puede haber un bit en el alambre en cualquier instante y, por lo general, el tiempo se dibuja empezando por la izquierda y avanzando hacia la derecha. Esto produce un gráfico de bits lógicos contra tiempo de la transmisión en serie, al cual se le conoce como diagrama de tiempos. Observe que en esta presentación el bit menos significativo se muestra a la izquierda, ya que se envió primero.

La principal diferencia entre las representaciones en paralelo y en serie es la pérdida de velocidad a cambio de simpleza en el circuito. La transmisión de datos binarios desde una parte del sistema digital a otra puede realizarse con más rapidez si se utiliza el método en paralelo ya que todos los bits se transmiten al mismo tiempo, mientras que en el método serie se transmite un bit a la vez. Por otro lado, la transmisión en paralelo requiere más líneas de señal conectadas entre el emisor y el receptor de los datos binarios que la transmisión en serie. En otras palabras, la transmisión en paralelo es más rápida y la transmisión en serie requiere menos líneas de señal. A lo largo del libro encontraremos muchas veces esta comparación entre los métodos paralelo y serie para representar información binaria.